[wpforms id="548" title="false" description="false"]

Successful activity since 2004!
We have 69 objects of intellectual property
Cooperation with leading universities, specialized publications and standardization committees
Solutions for various industries
Long-term experience of profitable cooperation
We are scientists
We are developers
In 2015 Nordavind Group entered the market of telemedicine with a unique mobile complex for self-monitoring of the cardiovascular system.
During 3 years 3 devices have been developed: ECG Dongle, ECG Dongle Full and holter monitor “RHYTHM”, mobile application and cloud service “CardioCloud”. 2 devices have been started in batch production.
Over 12 000 devices were released, the mobile application was downloaded more than 1500 times, cardiologists in the cloud service decoded more than 1300 electrocardiograms.
ECG Dongle is the winner of the contest "Made in Moscow".
Electrocardiographs ECG Dongle and ECG Dongle Full are used in 82 countries.
Over 12 000 devices were released, the mobile application was downloaded more than 1500 times, cardiologists in the cloud service decoded more than 1300 electrocardiograms.
ECG Dongle is the winner of the contest "Made in Moscow".
Electrocardiographs ECG Dongle and ECG Dongle Full are used in 82 countries.

Since 2017 we have been developing in the field of Blockchain
We created:
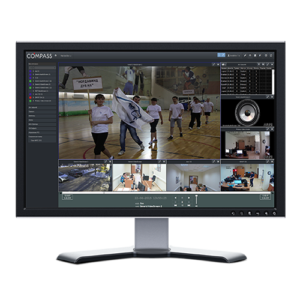
We are pioneers in the market of software solutions for the organization of Linux-based video surveillance systems.
Our first product – CCT “TeleWizard” was introduced in 2004.
At present the list of developed solutions in the field of intelligent video analytics has 10 basic products and many adapted versions for specific tasks.
At present the list of developed solutions in the field of intelligent video analytics has 10 basic products and many adapted versions for specific tasks.
We are partners
The multi-purpose group of companies “Nordavind” was created in 2004.
- We have carried out more than 100 projects for our customers, including the Russian Ministry of Internal Affairs, Rostelecom, Sberbank and PhosAgro.
- We received more than 24 letters of gratitude for time and work quality. Our products were highly appreciated not only by customers, but also by industry experts in which we work: we have 19 awards and 19 diplomas in video analytics and 4 awards in telemedicine.
Our team
Contacts
Actual contacts:
Moscow:
- Moscow, Butlerova str. 17, BC NEO GEO, Building B
- [email protected]
- +7 (499) 130-98-92
Dubna:
- Dubna, Programmistov str. 4, office 325
- [email protected]
- +7 (499) 608-01-88



































































